E155 Lab 7: Hardware Accelerated AES-128 Encryption
Introduction
In this lab, the MCU and FPGA were used together to implement a hardware-accelerated version of the Advanced Encryption Standard (AES) for 128-bit data encryption. The MCU stored the plaintext, cipher key, and expected ciphertext, and transmitted the plaintext and key to the FPGA via the SPI interface. The FPGA performed the AES encryption according to the NIST-197 standard and then returned the resulting ciphertext to the MCU. Finally, the MCU compared the received ciphertext to the expected value and indicated the success or failure of the encryption process through output signals lighting either a green (success) or red (failure) LED.
AES Overview
AES is a symmetric encryption algorithm that uses a specific key to both encrypt and decrypt data. It is the global standard for secure data encryption and is defined in three key sizes: AES-128, AES-192, and AES-256, where the number indicates the bit length of the cipher key. A larger key size provides stronger security but requires more hardware resources. AES encrypts data through a sequence of sub-algorithms and transformations that repeatedly mix the key with the plaintext to produce a ciphertext that appears random and cannot be reversed without the correct key. These transformations operate on matrices of bytes, with the key itself acting as one of the main transformation matrices. The encryption process consists of four main operations:
- SubBytes(): performs a non-linear byte substitution using a 16×16 S-box lookup table.
- shiftRows(): cyclically shifts the rows of the state matrix by varying offsets depending on row.
- mixColumns(): transforms each column of the state matrix using Galois Field arithmetic to further diffuse the data.
- AddRoundKey(): combines the current state with a round key using a bitwise XOR operation.
Finally, these operations are repeated across multiple rounds of encryption, each using a different round key derived through an algorithm known as keyExpansion(). In the AES-128 implementation used in this lab, the encryption involves 10 rounds. Each round follows the sequence: AddRoundKey → SubBytes → ShiftRows → MixColumns, with the final round (10) skipping the MixColumns step.
Experiment Setup and Design Overview
MCU Setup
The MCU was already configured through the provided starter code. It was configured to implement the SPI mode 1. It was also set up as the master with an artificial chip select signal to allow 8-bit CE-based SPI decoding on the logic analyzers. The MCU controlled the internal signals that started the SPI transactions as well as checked results from the transactions. The MCU would set the signal load to the FPGA that prepares it to recieve inputs. The MCU then sends the plaintext and then the cipherkey and then would set load LOW to signal that all data is sent. During that period, the FPGA performs encryption and once all 10 rounds complete, the FPA sets the signal done HIGH so that the MCU prepares to receive the ciphertext. Once received, the MCU compared it to the expected cipher through a difference operation. If all operations yield zero, the green LED through PA9 would light up, otherwise the red LED at P10 lights up indicating that encryption didn’t work properly. This process was always triggered using the MCU reset that restarted the transactions.
FPGA Setup
Since all encryption was done by the FPGA, we had to write SystemVerilog modules to perform the transformation operations necessary for executing the AES encryption. A lot of these operations required heavy resource usage as operations such as key expansion are applied across a 128-bit word. This would always run the risk of exhausting LUTs and other FPGA resources. Therefore I had to take into account how my logic synthesized to ensure the implied hardware isn’t too heavy for the FPGA. The subBytes() lookup table was loaded into the FPGA embedded block RAMs which have the ability to store files upto 128kB. To ensure it is mapped properly to the EBRs, we used a clocked version of the AES byte substitution algorithm named sbox_sync(). This module could only parse an 8-bit word so in subBytes(), it was called 16 times to parse the full 128-bit word. The shiftRows() module performed some row permutation by rotating the 4 rows: row 0 was kept as is, row 1 was shifted left by 1, row 2 by 2, and row 3 by 3. After row permutation, mixColumns() treats each state as a four-byte vector and performs matrix multiplication (Galois field operations) on the bytes in a column withinin \(GF(2^8)\) followed by XOR operations to handle overflows. Next up is the addRoundKey() that performs XOR operations between the 128-bit word and the 128-bit key. Finally, I wrote down the module getNextKey() which performed the key expansion part of AES which receives a 128-bit key value and the tound constant, rcon, which is a series of 4-byte words used in the key schedule to create the sub-keys for each encryption round. The module would determine the key for the next round following the implementation and pseudocode provided in the standards document.
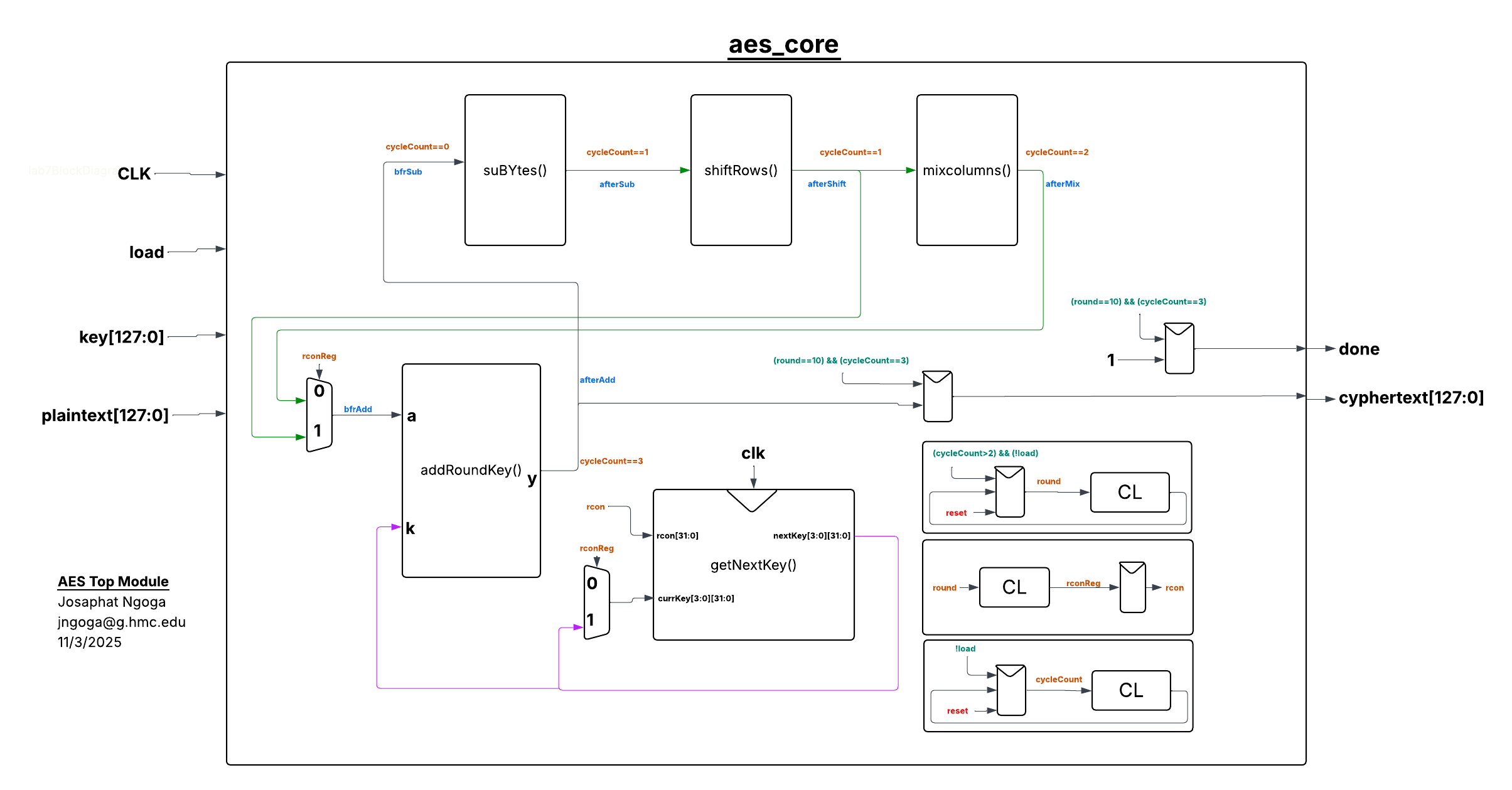
All the submodules described above were combined in a module named aes_core() whose job was implement the encryption datapath. The datapath followed the structure described in the AES Overview section above. The module took in the load signal that is asserted by the MCU after sending the plaintext and key, then initiated the process. The FPGa would continously reset/update internal signals as long as load was HIGH. For round 0, the plaintext is XORed with the key and the result is passed on to the next rounds. In rounds 1 to 9, the key is updated each round alongside the the input to the datapath. This input is represented in the code as state as it hold the intermediate states of the data in-between rounds. After round 10, the done signal is asserted to prepare the MCU to receive the cyphertext.
Using a synchronized sbox meant that it takes multiple cycles per round to process the data sequentially and safely propagate signals through the combinational logic. Therefore I used cycleCountto basically set when to take inputs, when to latch outputs and when to move to the next rounds. The cycle count was also to help account for the single cycle delay caused by subBytes(). Without it, the datapath would race and try to perform key operations before byte substitution stabilizes.
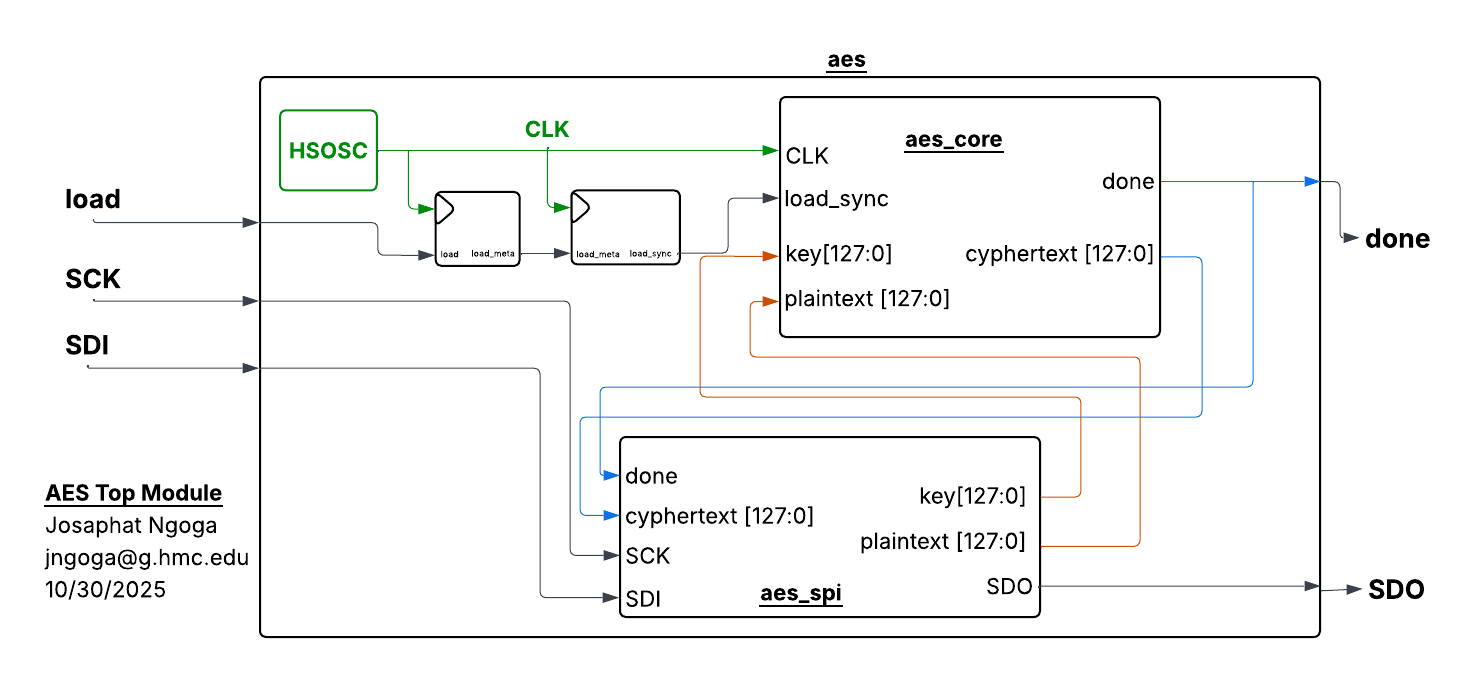
To run the setup, we implemented the aes() module that prompts both aes_core() and the aes_spi() module that executes SPI communication betweent both the MCU and the FPGA. Since data is received by the FPGA based on SCK from the FPGA, I added a synchronizer that ensures the load signal referenced by the FPGA for encryption, is latched on the rising edge of the internal clock (HSOSC/clk) instead of the SPI clock domain. This eliminated a synchronization error where encryption would be randomly true/false depending on the data latched. The connection and signals between these modules is shown in Figure 1.
Design Implementation
The modules to enforce the AES encryption and those that control the respective encryption transformation algorithms were written in SystemVerilog to run on the FPGA. To ensure proper communication and signal control between the MCU and FPGA, all signals followed the hierachy in the block diagram below:
aes_core() involves multiple blocks and enabler logic that manages the flow of signals and data through the different transformations within the datapath as shown in Figure 2 below:
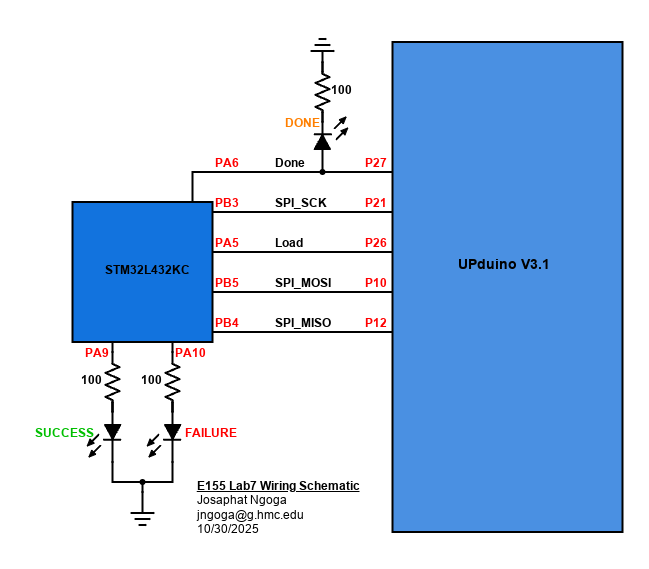
After running the simulation ensuring modules work as expected, the full setup was installed on the development board. The board has DIP switches that connect specific MCU pins to specific FPGA pins which reduces the need for crossing wires. Other necessary signals like the LEDs were setup on a side breadboard. The complete setup is shown in the following schematic:
Hardware Testing
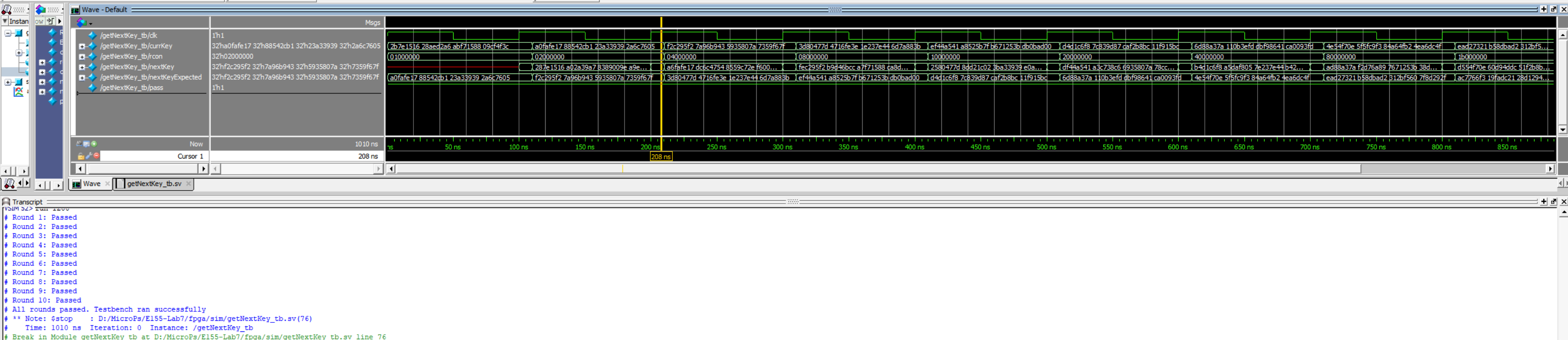
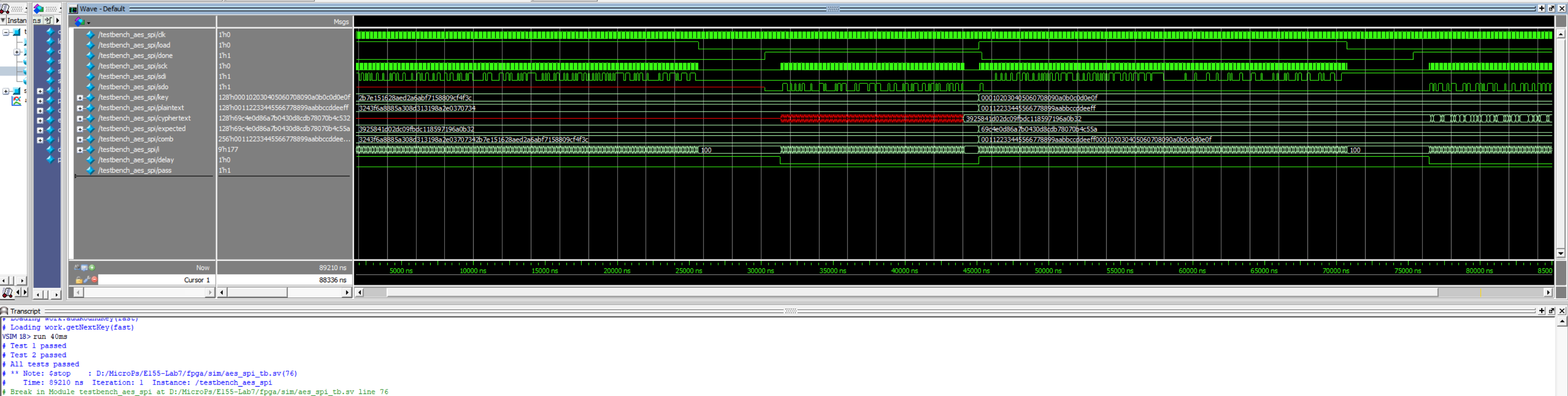
The testbenches were extremely helpful, especially for this particular lab. I was able to track how my key and other signals move around as I’m performing the key expansion. It allowed me to see how each data signal is loaded as well as when it is updated and it was how I realized the subBytes() issue. They were also essential in testing the modules that I had to write for this lab to ensure that the AES transformation modules function as expected. Each testbench was ran using examples from the NIST:197 Examples as well as other random hex values to check with more tests as possible.
NB: All testbenches were configured to run multiple trials to test consistency in execution and functionality hence the longer waves. Click on the relevant picture to zoom in on the wave traces.
The testbenches for all relevant modules are shown in the figures below:
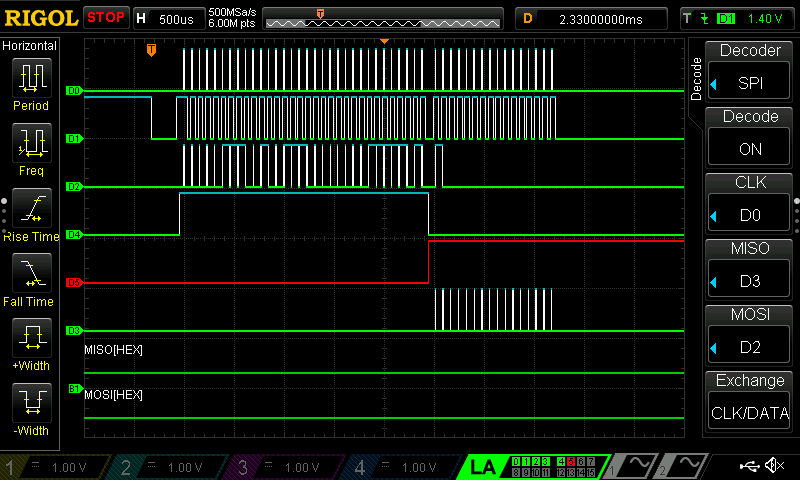
As shown from all the different tests and cases above, the hardware-accelerated AES logic is valid. To test the hardware, I used the a logic analyzer to visualize the SPI transactions and check the data shared between the MCU and the FPGA. We can see that load (D4) is HIGH during transfer and goes LOW at which point done (D5) goes high after encryption and FPGA starts sending data. The resulting waves are shown below:
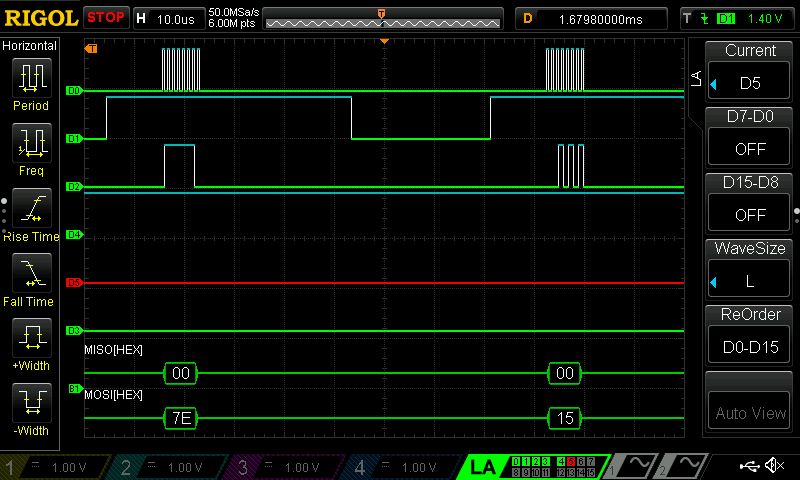
The zoomed in transaction shows that the MCU is at the stage of sending the key to the FPGA after which it will set the load signal LOW to begin encryption.
Conclusion
This lab took around 23 hours to complete. I lost a lot of time when implementing the key expansion logic because since I was using a split word (4x32) as opposed to the full 128-bit word it meant that my rotation had to apply to the “MSB” word. The standard states you rotate the “first word” but my interpretation of that led me to rotate the “LSB word” which was wrong. The second issue was that I didn’t implement properly the desired delay to help the subBytes() output stabilize therefore I was using wrong data in other blocks, sometimes not even have any data, especially in the first round (round0) and the middle round (round 5). I solved the issue by using a cycle counter, using a register to store intermediate round values. Finally, I had to fix a synchronization issue betwen the two clock domains (sck and clk) that would randomize the success of my encryption. Overall, it was amazing to learn the logic and intuition behing the Advanced Encryption Standard.
AI Prototype Summary
The goal of the AI prototype was to see if the AI can create the key expansion code of AES with instructions requesting that specifically or with instructions that give details without explicitly stating AES.
// -----------------------------------------------------------------------------
// AES-128 Key Expansion: single "round step"
// next_key = KeyExpansion(prev_key, round_idx)
// FIPS-197: w'[0] = w[0] ^ (SubWord(RotWord(w[3])) ^ Rcon[i])
// w'[1] = w[1] ^ w'[0]
// w'[2] = w[2] ^ w'[1]
// w'[3] = w[3] ^ w'[2]
// Notes:
// - prev_key and next_key are 4 words (w[0]..w[3]), each 32 bits.
// - round_idx is 1..10 for AES-128.
// - Rcon[i] is {rc, 8'h00, 8'h00, 8'h00} with rc sequence per FIPS-197.
// -----------------------------------------------------------------------------
module aes128_key_expand_round
(
input logic [3:0][31:0] prev_key, // prev_key[0] is w[0] (MS 32 bits), prev_key[3] is w[3] (LS 32 bits)
input logic [3:0] round_idx, // valid: 1..10
output logic [3:0][31:0] next_key
);
// --- g() = SubWord(RotWord(w[3])) ^ Rcon[i] ---
logic [31:0] w3_rot;
logic [31:0] w3_sub;
logic [31:0] rcon_word;
logic [31:0] gword;
// Assume these two modules are provided elsewhere and are purely combinational:
// RotWord: rotates left by 8 bits: {w[23:0], w[31:24]}
// SubWord: applies the S-box to each byte of the word
RotWord u_rot (.in(prev_key[3]), .out(w3_rot));
SubWord u_sub (.in(w3_rot), .out(w3_sub));
// Rcon lookup (top byte only; other bytes are 0)
always_comb begin
unique case (round_idx)
4'd1: rcon_word = 32'h01_00_00_00;
4'd2: rcon_word = 32'h02_00_00_00;
4'd3: rcon_word = 32'h04_00_00_00;
4'd4: rcon_word = 32'h08_00_00_00;
4'd5: rcon_word = 32'h10_00_00_00;
4'd6: rcon_word = 32'h20_00_00_00;
4'd7: rcon_word = 32'h40_00_00_00;
4'd8: rcon_word = 32'h80_00_00_00;
4'd9: rcon_word = 32'h1B_00_00_00;
4'd10: rcon_word = 32'h36_00_00_00;
default: rcon_word = 32'h00_00_00_00; // safe default
endcase
end
assign gword = w3_sub ^ rcon_word;
// Next key words per FIPS-197
assign next_key[0] = prev_key[0] ^ gword;
assign next_key[1] = prev_key[1] ^ next_key[0];
assign next_key[2] = prev_key[2] ^ next_key[1];
assign next_key[3] = prev_key[3] ^ next_key[2];
endmoduleThe execution of the key expansion logic is valid and I was able to verify it with my testbench and surprisingly it passed on the first try which I would say is a first for an LLM writing a code like this. But then I guess that since it was specifically noted that this is AES, there is enough information on the internet for it to properly execute key expansion.
// Assumptions about existing blocks:
// module module1(input logic [31:0] in, output logic [31:0] out);
// module module2(input logic [31:0] in, output logic [31:0] out);
module key_schedule #(
parameter int NK = 4, // number of initial 32-bit words from key
parameter int NR = 10 // number of "rounds" controlling total words
) (
// key holds NK words, packed left-to-right as:
// key[32*NK-1 -: 32] = w[0], key[32*(NK-1)-1 -: 32] = w[1], ... (see slice below)
input logic [32*NK-1:0] key,
// Rcon indexed by i/NK; must be large enough for max i
// Required length = (4*NR+3)/NK + 1 (integer division)
input logic [31:0] Rcon [0:((4*NR+3)/NK)],
// Output schedule: words w[0 .. 4*NR+3], each 32-bit
output logic [31:0] w [0:(4*NR+3)]
);
localparam int MAX_I = 4*NR + 3;
localparam bit NK_GT6 = (NK > 6);
// Helper: extract the i-th 32-bit word from 'key' for i in [0..NK-1]
// w[i] <- key[4*i .. 4*i+3] (treating each w[i] as 32 bits)
function automatic logic [31:0] key_word(input int idx);
// Map i -> 32-bit slice; here we choose MSB-first packing:
// key[32*NK-1 -: 32] = w[0], key[32*NK-33 -: 32] = w[1], ...
key_word = key[32*(NK-idx)-1 -: 32];
endfunction
// Unrolled construction of all words
genvar i;
generate
for (i = 0; i <= MAX_I; i++) begin : gen_words
if (i < NK) begin : init_words
// Initialization: w[i] <- key[4*i..4*i+3]
always_comb w[i] = key_word(i);
end
else begin : recur_words
// temp <- w[i-1]
logic [31:0] temp0;
logic [31:0] after_m2;
logic [31:0] after_m1;
logic [31:0] after_m1_only;
logic [31:0] temp_sel;
// Previous word
always_comb temp0 = w[i-1];
// Instantiate transforms only where needed (compile-time conditions)
if ((i % NK) == 0) begin : do_m2_then_m1_and_xor_rcon
module2 u_m2 (.in(temp0), .out(after_m2));
module1 u_m1 (.in(after_m2), .out(after_m1));
// temp <- module1(module2(temp)) (+) Rcon[i/NK]
always_comb temp_sel = after_m1 ^ Rcon[i / NK];
end
else if (NK_GT6 && ((i % NK) == 4)) begin : do_m1_only
module1 u_m1_only (.in(temp0), .out(after_m1_only));
// temp <- module1(temp)
always_comb temp_sel = after_m1_only;
end
else begin : pass_through
// temp unchanged
always_comb temp_sel = temp0;
end
// w[i] <- w[i-NK] (+) temp
always_comb w[i] = w[i-NK] ^ temp_sel;
end
end
endgenerate
endmodule